Predictions of ACE's surveying results

Carl Shulman is polling people about their predictions for the results of the upcoming ACE study to encourage less biased interpretations. Here are mine.

Assuming control group follows the data in e.g. the Iowa Women's Health Study they should eat 166g meat/day with sd 66g.¹ (For the rest of this post, I'm going to assume everything is normally distributed, even though I realize that's not completely true.)

For mathematical ease, let's take our prior from the farm sanctuary study and say: 2% are now veg, and an additional 5% eat "a lot less" meat which I'll define as cutting in half. So the mean of this group is 159g (4.2% less) w/ sd 69g.

I don't know what tests they will do, but let's look at a t-test because that's easiest. The test statistic here is:
$$t=\frac{166-159}{\sqrt{\frac{66}{N_1}+\frac{69}{N_2}}}$$
Let's assume 5% of those surveyed were in the intervention group. Solving for $N$ in
$$1.96=\frac{7}{\sqrt{\frac{66}{.95N}+\frac{69}{.05N}}}$$
we find $N\approx 350$, meaning that I expect the null hypothesis to be rejected at the usual $\alpha=.05$ if they collected at least 350 survey responses.² I'm leaning slightly towards it not being significant, but I'm not sure how much data they collected.

Here's my estimate of their estimate (I can't do this analytically, so this is based on simulations):

You can see that the expected outcome is the true difference of about 4 veg equivalents per 100 leaflets, but with such a small sample size there is a 25% chance that we'll find leafleted people were less likely to go veg.

Here's how a 50% confidence interval might shake out:

The left graph is the bottom of the CI, the right one is the top.

Putting Money where my Mouth Is

The point of this is so that I don't retro-justify my beliefs, which is that meta-research in animal-related fields is the most effective thing. I have a lot of model uncertainty, but I would broadly endorse the conclusions of the above. The following represent ~2.5% probability events (each), which I will take as evidence I'm wrong.

• If a 50% CI is exclusively above 9 veg equivalents per 100 leaflets, then I think its ability to attract people to veganism outweighs the knowledge we'd gain from more studies. Therefore, I pledge $1,000 to VO or THL (or whatever top-ranked leafleting charity exists at the time).
• If a 50% CI is exclusively below zero, then veg interventions in general are less useful than I thought. Therefore I pledge $1,000 to MIRI (or another x-risk charity, if e.g. GiveWell Labs has a recommendation by then).

I don't think my above model is completely correct, and I'm sure ACE will have a different parameterization, so I don't know that these are really the 5% tails, but I would consider either of them to be a surprising enough event that my current beliefs are probably wrong.

I am open to friendly charity bets (if result is worse than X I give money to your charity, else you give to mine), if anyone else is interested.

Footnotes

1. I tried to use MLE to combine multiple analyses, but found that the standard deviation is > 10,000 g/day. It's a good thing ACE has professional statisticians on the job, because the data clearly is kind of complex.
2. I used $d.f.=\infty$

An Improvement to "The Impossibility of a Satisfactory Population Ethics"

Gustaf Arrhenius has published a series of impossibility theorems involving ethics. His most recent is The Impossibility of a Satisfactory Population Ethics which basically shows that several intuitive premises yield a stronger version of the repugnant conclusion.

If you know me, you know that I believe that modern ("abstract") algebra can help resolve problems in ethics. This is one example: using some basic algebra, we can get a stronger result than Arrhenius while using weaker axioms.

This is a "standing on the shoulders of giants" type of result: mathematicians have had centuries to trim their axioms to the minimal required set, so once you're able to phrase your question in more standard notation you can quickly arrive at better conclusions. Similarly, the errors in Arrhenius' proof that I've noted in the footnotes are mostly errors of omission that many extremely smart people made, until others pointed out pathological cases where their assumptions were invalid.

Assumptions

We assume that it's possible to have lives that are worth living ("positive" welfare), lives not worth living ("negative" welfare) and ones on the margin ("neutral" welfare). Arrhenius doesn't specify what the relationship is between "positive" and "negative" welfare, but I think there's a very intuitive answer: they cancel each other out. Just as $(+1) + (-1) = 0$, a world with a person of $+1$ utility and one with $-1$ utility is equivalent to a world with people at the neutral level.¹

We continue the analogy with addition by writing $Z=X+Y$ if $Z$ is the union of two populations $X$ and $Y$. Just as with normal addition, we assume that $X+Y$ is always defined² and that we can move parentheses around however we want, i.e. $(X+Y)+Z=X+(Y+Z)$. Lastly, I'm going to assume that the order in which you add people doesn't matter, i.e. $X+Y=Y+X$.³ I will finish the analogy with addition by specifying that welfare is isomorphic to the integers.⁴

(The above is just a long-winded way of saying that population ethics is isomorphic to the free abelian group on $\mathbb Z$.)

Also, for simplicity, I will write $nX$ for $\underbrace{X+\dots+X}_{n\ times}$.⁵

Lastly, we need to define our ordering. I'll use the notation that $X\leq Y$ means "Population $X$ is morally worse than population $Y$" and require that $\leq$ is a quasi-order, i.e. $X\leq X$ and $X\leq Y, Y\leq Z$ implies that $X\leq Z$. Notably, this does not require us to believe that populations are totally ordered, i.e. there may be cases where we aren't sure which population is better.

The major controversial assumption we need from Arrhenius is what he calls "non-elitism": for any $X,Y$ with $X-1>Y$ there is an $n>0$ such that for any population $D$ consisting of people with welfare levels between $X$ and $Y$: $(n+1)(X-1)+D\geq X+nY+D$. In less formal terms, this is basically saying that there are no "infinitely good" welfare levels.

Claim

We claim that any group following the above axioms results in:

The Very Repugnant Conclusion: For any perfectly equal population
with very high positive welfare, and for any number of lives with very
negative welfare, there is a population consisting of the lives with negative welfare and lives with very low positive welfare which is better than the high welfare population, all things being equal.

Unused Assumptions

The following are assumptions Arrhenius makes which are unused. (Note: these are verbatim quotes from his paper, unlike the other assumptions.)

(Exercise for the advanced reader: figure out which of these also follow from the assumptions we did use.)

1. The Egalitarian Dominance Condition: If population A is a perfectly
   equal population of the same size as population B, and every person in
   A has higher welfare than every person in B, then A is better than B,
   other things being equal.
2. The General Non-Extreme Priority Condition: There is a number n
   of lives such that for any population X, and any welfare level A, a
   population consisting of the X-lives, n lives with very high welfare, and
   one life with welfare A, is at least as good as a population consisting
   of the X-lives, n lives with very low positive welfare, and one life with
   welfare slightly above A, other things being equal.
3. The Weak Non-Sadism Condition: There is a negative welfare level and
   a number of lives at this level such that an addition of any number of
   people with positive welfare is at least as good as an addition of the
   lives with negative welfare, other things being equal.

Proof

Lemma

First we prove a lemma: what Arrhenius calls "Condition $\beta$" and what mathematicians would refer to as a proof that our group is Archimedean. This means that for any $X,Y>0$ there is an $n$ such that $nX\geq Y$.

Basically we just observe that the "non-elitism" condition makes a simple induction. Starting from the premise that $(n+1)(X-1)+D\geq X+nY+D$, let $Y, D=0$, giving us that $(n+1)(X-1)\geq X$, i.e. $X$ is Archimedean with respect to $X-1$. Continuing the induction we find that $X$ is Archimedean with respect to $X-k$, completing the proof.^6,7

Theorem

First, let me give a formal definition of the "Very Repugnant Conclusion": For any high level of welfare $H$, low positive level of welfare $L$ and negative level of welfare $-N$ and population sizes $c_{H},c_{N}$ there is some $c_{L}$ such that $c_{L}\cdot L+c_{N}\cdot(-N)\geq c_{H}H$.

To prove our claim: we know there is some $k_{1}$ such that
$$k_{1}\cdot L\geq c_{H}\cdot H\label{ref1}$$
because of our lemma. Because it's a group, we know that $(N+-N)+L=L$ and moreover $(c_{N}N+c_{N}\cdot-N)+L=L$. Substituting this into (1) yields
$$k_{1}\left[\left(c_{N}N+c_{N}\cdot-N\right)+L\right]\geq c_{H}H\label{ref2}$$
Expanding the left hand side of (2) we get
$$k_{1}c_{N}N+k_{1}c_{N}\cdot(-N)+k_{1}L\label{ref3}$$
By our lemma there is some $k_{2}$ such that $k_{2}L+D\geq k_{1}c_{N}N+D$; letting $D=k_{1}c_{N}(-N)+k_{1}L$ and using transitivity we get that
$$k_{2}L+k_{1}c_{N}(-N)+k_{1}L\geq c_{H}H$$
Rewriting terms leaves us with
$$\left(k_{1}+k_{2}\right)L+k_{1}c_{N}(-N)\geq c_{H}H$$
or
$$c_L L+c_{N'}(-N)\geq c_{H}H$$
$\blacksquare$

Comments

I don't know that this shorter proof is much more convincing than Arrhenius' - my guess is that the people who disagree with an assumption are those who take a "person-affecting" view or otherwise object to the entire premise of the theorem. I would though say that:

1. None of the math I've used is beyond the average high-school student. It's just making the "algebra can be about things other than numbers" leap which is hard.
2. While abstract algebraic notation can be intimidating, it's relevant to realize that using it makes you more concise. (To the extent that a 26-page paper can be rewritten into a two-page blog post.)
3. Because we can be more concise and use standard terminology, it shines a light on what is really the controversial assumption: Non-Elitism.
4. Similarly, because we use standard concepts it's easier to see missing assumptions (e.g. I didn't realize that Arrhenius was missing a closure axiom until I tried to cast it in group theory terms).

Lastly, because I can't finish any post without mentioning lattice theory, I'll add that some of the errors in Arrhenius' paper occurred because lattices are such a natural structure that he assumed they exist even where they weren't shown to. Of course, if you involve lattices more you end up with total utilitarianism, giving more insight into why Arrhenius' result holds.

Acknowledgements

I would like to thank Prof. Arrhenius for the idea, and Nick Beckstead for talking about it with me.

Footnotes

1. Formally, for each $X$ there is some $-X$ such that for all $Y$, $X+(-X)+Y=Y$.
2. This isn't an explicit assumption in Arrhenius, but it's implicitly assumed just about everywhere
3. This arguably is controversial so I'll point out that commutativity isn't really required, but since it keeps the proof a lot shorter and most people will accept it, I'll keep the assumption
4. Arrhenius "proves" that welfare is order-isomorphic to $\mathbb Z$ incorrectly, so I'll just assume it instead of attempting to derive it from others. If you prefer, you can take his "Discreteness" axiom, add in assumptions that welfare is totally ordered and has no least or greatest element and you'll get the same thing.
5. Which is just to say that since it's an abelian group it's also a $\mathbb Z$-module.
6. Nick Beckstead thought that some people might not like using the neutral level like this, so I'll point out that you can use an alternative proof at the expense of an additional axiom. If you assume non-sadism, then you can find that $X+nY\geq X$ and therefore transitively $(n+1)(X-1)\geq X$.
7. This is somewhat misleading: we've only shown that the group is archimedean for totally equitable populations. That's all we need though.

How Conscious is my Relationship?

One of the most interesting theories of consciousness is Integrated Information Theory (IIT), proposed by Giulio Tononi. One of its more radical claims is that consciousness is a spectrum, and that virtually everything in the universe from the smallest atom to the largest galaxy has at least some amount of consciousness.

Whatever criticisms one can make of IIT, the fact that it allows you to sit down and calculate how conscious a system is represents a fundamental advance in psychology. Since people say that good communication is the most important part of a relationship, and since any information-bearing system's consciousness can be calculated with IIT, I thought it would be fun to calculate how conscious Gina and my's relationship is.

A Crash Course on Information

Entropy
The fundamental measure of information is surprise. The news could be filled with stories about how gravity remains constant, the sun rose from the east instead of the west and the moon continues to orbit the earth, but there is essentially zero surprise in these stories, and hence no information. If the moon were to escape earth's orbit we would all be shocked, and hence get a lot of information from this.

Written words have information too. If I forget to type the last letter of this phras, you can probably still guess it, meaning that trailing 'e' carries little surprise/information. Claude Shannon, founder of information theory, did precisely this experiment, covering up parts of words and seeing how well one could guess the remainder. (English has around 1 bit of information per letter, for the record.)

Whatever you're dealing with the important part to remember is that "surprise" is when a low-probability event occurs, and that "information" is proportional to "surprise". Systems which can be predicted very well in advance, such as whether the sun rises from the east or the west, have very low surprise on average. Those which cannot be predicted, such as the toss of a coin, have much more surprising outcomes. (Maximally surprising probability distributions are those where every event is equally likely.) The measure of how surprising a system is (and hence how much information the system has) was named Entropy by Shannon based on von Neumann's advice that "no one knows what entropy really is, so in a debate you will always have the advantage".

Divergence
Someone who knows modern English will have a bit more surprise than usual upon reading Shakespeare - words starting with "th" will end in "ou" more often than one would expect, but overall it's not too bad. Chaucer's Canterbury tales one can struggle through with difficulty, and Caedmon (the oldest known English poem) is so unfamiliar the letters are essentially unpredictable:

nu scylun hergan hefaenricaes uard
metudæs maecti end his modgidanc
uerc uuldurfadur swe he uundra gihwaes
eci dryctin or astelidæ
- first four lines of Caedmon. Yes, this is considered "English".

If we approximate the frequency of letters in Shakespeare based on our knowledge of modern English we won't get it too wrong (i.e. we won't frequently be surprised). But our approximation of Caedmon from modern English is horrific - we're surprised that 'u' is followed by 'u' in "uundra" and that 'd' is followed by 'æ' in "astelidæ".

Since you can make a good estimate of letter's frequencies in Shakespeare based on modern English, that means Shakespearean English and modern English have a low divergence. The fact that we're so frequently described when reading Caedmon means that the probability distribution there is highly divergent from modern English.

Consciousness

Believe it or not, Entropy and Divergence are the tools we need to calculate a system's consciousness. Roughly, we want to approximate a system's behavior by assuming that its constituent parts behave independently. The worse that approximation is, the more "integrated" we say the system is. Knowing that, we can derive its Phi, the measure of its consciousness.

Our Relationship as a Conscious Being

Here is a completely unscientific measure of mine and Gina's behavior over the last day or so:

The (i,j) entry is the fraction of time that I was doing activity i and Gina was doing activity j. (The marginal distributions are written, appropriately enough, in the margins.)

You can see that my entropy is 1.49 bits, while Gina (being the unpredictable radical she is) has 1.69 bits. This means that our lives are slightly less surprising than the result of two coin tosses (I can hear the tabloids knocking already).

However, our behavior is highly integrated: like many couples in which one person is loud and the other is a light sleeper, we're awake at the same time, and our shared hatred of driving means we only travel to see friends as a pair. Here's how it would look if we didn't coordinate our actions (i.e. assuming independence):

The divergence between these two distributions is our relationship's consciousness (Phi). Some not-terribly-interesting computations show that Phi = 1.49 bits.

The Pauli exclusion principle tells us that electrons in the innermost shell have 1 bit of consciousness (i.e. Phi = 1), meaning that our relationship is about as sentient as the average helium atom. So if we do decide to break up, the murder of our relationship won't be much of a crime.

Side Notes

Obviously this is a little tongue-in-cheek, but one important thing you might wonder is why my decision to consider our relationship to have two components (me and Gina) is the correct one. Wouldn't it be better to assume that there are 200 billion elements (one for each neuron in our brains) or even 10²⁸ (one for each atom in our bodies)?

The answer is that yes, that would be better (apart from the obvious computational difficulties). IIT says that consciousness occurs at the level of the system with the highest value of Phi, so if we performed the computation correctly, we would of course find that it's Gina and myself who are conscious, not our relationship, since we have higher values of Phi.

(The commitment-phobic will notice a downside to this principle: if your relationship becomes so complex and integrated that its value of Phi exceeds your own, you and your partner would lose individual consciousness and become one joint entity!)

I should also note that I've discussed IIT's description of the quantity of consciousness, but not its definition of quality of consciousness.

Conclusion

Our beliefs about consciousness are so contradictory it's impossible for any rigorous theory to support them all, and IIT does not disappoint on the "surprising conclusions" front. But some of its predictions have been confirmed by evidence (the areas of the brain with highest values of Phi are more linked to phenomenal consciousness, for example) and the fact that it can even make empirical predictions makes it an important step forward. I'll close with Tononi's description of how IIT changes our perspective on physics:

We are by now used to considering the universe as a vast empty space that contains enormous conglomerations of mass, charge, and energy—giant bright entities (where brightness reflects energy or mass) from planets to stars to galaxies. In this view (that is, in terms of mass, charge, or energy), each of us constitutes an extremely small, dim portion of what exists—indeed, hardly more than a speck of dust.

However, if consciousness (i.e., integrated information) exists as a fundamental property, an equally valid view of the universe is this: a vast empty space that contains mostly nothing, and occasionally just specks of integrated information (Φ)—mere dust, indeed—even there where the mass-charge–energy perspective reveals huge conglomerates. On the other hand, one small corner of the known universe contains a remarkable concentration of extremely bright entities (where brightness reflects high Φ), orders of magnitude brighter than anything around them. Each bright “Φ-star” is the main complex of an individual human being (and most likely, of individual animals). I argue that such Φ-centric view is at least as valid as that of a universe dominated by mass, charge, and energy. In fact, it may be more valid, since to be highly conscious (to have high Φ) implies that there is something it is like to be you, whereas if you just have high mass, charge, or energy, there may be little or nothing it is like to be you. From this standpoint, it would seem that entities with high Φ exist in a stronger sense than entities of high mass.

Acknowledgements

The idea for this post came from Brian's essay on Suffering Subroutines, and the basis for my description of IIT came from Tononi's Consciousness as Integrated Information: a Provisional Manifesto. Gina read an earlier draft of this post.

A Pure Math Argument for Total Utilitarianism

Addition is a very special operation. Despite the wide variety of esoteric mathematical objects known to us today, none of them have the basic desirable properties of grade-school arithmetic.

This fact was intuited by 19th century philosophers in the development of what we now call "total" utilitarianism. In this ethical system, we can assign each person a real number to indicate their welfare, and the value of an entire population is the sum of each individuals' welfare.

Using modern mathematics, we can now prove the intuition of Mills and Bentham: because addition is so special, any ethical system which is in a certain technical sense "reasonable" is equivalent to total utilitarianism.

What do we mean by ethics?

The most basic premise is that we have some way of ordering individual lives.

We don't need to say how much better some life is than another, we just need to be able to put them in order. We might have some uncertainty as to which of two lives is better:

In this case, we aren't certain if "Medium" or "Medium 2" is better. However, we know they're both better than "Bad" and worse than "Good".

In the case when we always know which of two lives is better, we say that lives are totally ordered. If there is uncertainty, we say they are lattice ordered.

In either case, we require that the ranking remain consistent when we add people to the population. Here we add a person of "Medium" utility to each population:

The ranking on the right side of the figure above is legitimate because it keeps the order - if some life X is worse than Y, then (X + Medium) is still worse than (Y + Medium). This ranking below for example would fail that:

This ranking is inconsistent because it sometimes says that "Bad" is worse than "Medium" and other times says "Bad" is better than "Medium". A basic principle of ethics is that rankings should be consistent, and so rankings like the latter are excluded.

Increasing population size

The most obvious way of defining an ethics of populations is to just take an ordering of individual lives and "glue them together" in an order-preserving way, like I did above. This generates what mathematicians would call the free group. (The only tricky part is that we need good and bad lives to "cancel out", something which I've talked about before.)

It turns out that merely gluing populations together in this way gives us a highly structured object known as a "lattice-ordered group". Here is a snippet of the resulting lattice:

This ranking is similar to what philosophers often call "Dominance" - if everyone in population P is better off than everyone in population Q, then P is better than Q. However, this is somewhat stronger - it allows us to compare populations of different sizes, something that the traditional dominance criterion doesn't let us do.

Let's take a minute to think about what we've done. Using only the fact that individuals' lives can be ordered and the requirement that population ethics respects this ordering in a certain technical sense, we've derived a robust population ethics, about which we can prove many interesting things.

Getting to total utilitarianism

One obvious facet of the above ranking is that it's not total. For example, we don't know if "Very Good" is better than "Good, Good", i.e. if it's better to have welfare "spread out" across multiple people, or concentrated in one. This obviously prohibits us from claiming that we've derived total utilitarianism, because under that system we always know which is better.

However, we can still derive a form of total utilitarianism which is equivalent in a large set of scenarios. To do so, we need to use the idea of an embedding. This is merely a way of assigning each welfare level a number. Here is an example embedding:

• Medium = 1
• Good = 2
• Very Good = 3

Here's that same ordering, except I've tagged each population with the total "utility" resulting from that embedding:

This is clearly not identical to total utilitarianism - "Very Good" has a higher total utility than "Medium, Medium" but we don't know which is better, for example.

However, this ranking never disagrees with total utilitarianism - there is never a case where P is better than Q yet P has less total utility than Q.

Due to a surprising theorem of Holder which I have discussed before, as long as we disallow "infinitely good" populations, there is always some embedding like this. Thus, we can say that:

Total utilitarianism is the moral "baseline". There might be circumstances where we are uncertain whether or not P is better than Q, but if we are certain, then it must be that P has greater total utility than Q.

An application

Here is one consequence of these results. Many people, including myself, have the intuition that inequality is bad. In fact, it is so bad that there are circumstances where increasing equality is good even if people are, on average, worse off.

If we accept the premises of this blog post, this intuition simply cannot be correct. If the inequitable society has greater total utility, it must be at least as good as the equitable one.

Concluding remarks

There are certain restrictions we want the "addition" of a person to a population to obey. It turns out that there is only one way to obey them: by using grade school addition, i.e. total utilitarianism.

Double Your Effectiveness with a Bunny Suit

I decided today that three leafletters were saturating the area, so after I ran out of my first stack I just started tallying the other two's success. One was in a bright blue bunny costume, and the other was more normally dressed.

The bunny won (p = .0008).

	Accepted Leaflet	Declined Leaflet
Bunny Suit	20	11
No suit	18	47

Contingency table of what fraction of people accepted a leaflet when offered.

Who would you take a leaflet from?

A Graphical Introduction to Lattices

Here is my (extended) family tree:

Everyone in the tree shares at least one common ancestor and at least one common descendant. This makes my family tree a lattice, an important mathematical structure. While lattices are often presented in abstract algebraic form, they have a simple graphical representation called a Hasse diagram, which is similar to a family tree.

Because most lattice theory assumes a strong background in algebra, I think the results are not as well known as they should be. I hope to give a sampling of some lattices here, and a hint of their power.

What are Lattices?

A lattice is a structure with two requirements:

1. Every two elements have a "least upper bound." In the example above, this is the "most recent common ancestor".
2. Every two elements have a "greatest lower bound." In the example above, this is the "oldest common descendant".

Note that the bound of some elements can be themselves; e.g. the most recent common ancestor of me and my mother is my mother.

Lattices are a natural way of describing partial orders, i.e. cases where we sometimes know which element came "first", but sometimes don't. For example, because the most recent common ancestor of my mother and myself is my mother, we know who came "first" - my mother must be older. Because the least upper bound of my mother and my father is some third person, we don't know which one is older.

Shopping Carts

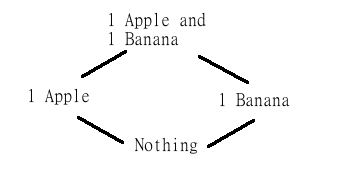
Here's an example of four different ways to fill your shopping cart:

The lines between two sets indicates preference: one apple is better than nothing, but one apple and one banana is even better than one apple. (Note that the arrows aren't directed, because every relation has a dual [e.g. the "better than" relation has a dual relation "worse than]. So whether you read the graph top-to-bottom or bottom-to-top, it doesn't really matter. By convention, things on the bottom are "less than" things on the top.)

Now, some people might prefer apples to bananas, and some might prefer bananas to apples, so we can't draw any lines between the "one apple" and the "one banana" situations. Nonetheless, we can still say that you prefer having both to just one, so this order is pretty universal.

The least upper bound in this case is "the worst shopping cart which is still preferred or equal to both things" (doesn't quite roll of the tongue, does it?), and the greatest lower bound is "the best shopping cart which is still worse than or equal to both things". Because these two operations exist, this means that shopping carts (or rather the goods that could be in shopping carts) make up a lattice.

A huge swath of economic and ethical problems deal with preferences which can be put into lattices like this, which makes lattice theory a powerful tool for solving these problems.

Division

This is a more classical "math" lattice:

Here a line between two integers indicates that the lower one is a factor of the higher one. The least upper bound in this lattice is the least common multiple (lcm) and the greatest lower bound is the greatest common divisor (gcd, some people call this the "greatest common factor").

The greatest common divisor of 4 and 10 is 2, and the least common multiple of 2 and 3 is 6.
Again we don't have a total ordering - 2 isn't a factor of 3 or vice versa - but we can still say something about the order.

An important set of questions about lattices deal with operations which don't change the lattice structure. For example, $k\cdot\gcd(x,y)=\gcd(kx,ky)$, so multiplying by an integer "preserves" this lattice.


Multiplying the lattice by three still preserves the divisibility relation.
A lot of facts about gcd/lcm in integer lattices are true in all lattices; e.g. the fact that $x\cdot y=\gcd(x,y)\cdot \text{lcm}(x,y)$.

Boolean Logic

Here is the simplest example of a lattice you'll probably ever see:

Suppose we describe this as saying "False is less than True". Then the operation AND becomes equivalent to the operation "min", and the operation OR becomes equivalent to the operation "max":

• A AND B = min{A, B}
• A OR B = max{A, B}

Note that this holds true of more elaborate equations, e.g. A AND (B OR C) = min{A, max{B, C}}. In fact, even more complicated Boolean algebras are lattices, so we can describe complex logical "gates" using the language of lattices.

Everything is Addition

I switch now from examples of lattices to a powerful theorem:

[Holder]: Every operation which preserves a lattice and doesn't use "incomparable" objects is equivalent to addition.¹

The proof of this is fairly complicated, but there's a famous example which shows that multiplication is equivalent to addition: logarithms.

The relevant fact about logarithms is that $\log(x\cdot y)=\log(x)+\log(y)$, meaning that the problem of multiplying $x$ and $y$ can be reduced to the problem of adding their logarithms. Older readers will remember that this trick was used by slide rules before there were electronic calculators.

Holder's theorem shows that similar tricks exist for any lattice-preserving operation.

Everything is a Set

Consider our division lattice from before (I've cut off a few numbers for simplicity):

Now replace each number with the set of all its factors:

We now have another lattice, where the relationship between each node is set inclusion. E.g. {2,1} is included in {4,2,1}, so there's a line between the two. You can see that we've made an equivalent lattice.

This holds true more generally: any lattice is equivalent to another lattice where the relationship is set inclusion.²

Max and Min Revisited

Consider the following statements from various areas of math:
$$\begin{eqnarray}
\max\{x,y\} & = & x & + & y & - & \min\{x,y\} &\text{ (Basic arithmetic)} \\
P(x\text{ OR } y) & = & P(x) & + & P(y) & - & P(x\text{ AND } y) & \text{ (Probability)} \\
I(x; y) & = & H(x) & + & H(y) & - & H(x,y) & \text{ (Information theory)} \\
\gcd(x,y) & = & x & \cdot & y & \div & \text{lcm}(x,y) & \text{ (Basic number theory)} \\
\end{eqnarray}$$When laid out like this, the similarities between these seemingly disconnected areas of math is obvious - these results all come from the basic lattice laws. It turns out that merely assuming a lattice-like structure for probability results in the sum, product and Bayes' rule of probability, giving an argument for the Bayesian interpretation of probability.

Conclusion

The problem with abstract algebraic results is that they require an abstract algebraic explanation. I hope I've managed to give you a taste of how lattices can be used, without requiring too much background knowledge.

If you're interested in learning more: Most of what I know about lattices comes from Glass' Partially Ordered Groups, which is great if you're already familiar with group theory, but not so great otherwise. Rota's The Many Lives of Lattice Theory gives a more technical overview of lattices (as well as an overview of why everyone who doesn't like lattices is an idiot) and J.B. Nation has some good notes on lattice theory, both of which require slightly less background. Literature about specific uses of lattices, such as in computer science or logic, also exists.

Footnotes

1. Formally, every l-group with only trivial convex subgroups is l-isomorphic to a subgroup of the reals under addition. Holder technically proved this fact for ordered groups, not lattice-ordered groups, but it's an immediate consequence.
2. By "equivalent" I mean l-isomorphic.

How to Create a Donor-Advised Fund

There are a lot of charities. So many, in fact, that some would-be altruists are struck with the alliterative analysis paralysis and end up not donating at all.

A tax vehicle known as a "Donor-advised fund" (DAF) allows you to get the best of both worlds: you can donate to charity, with all the psychological and tax benefits that go along with that decision, while still holding off on your decision as to which charity is best.

You can create your own DAF in about 15 minutes online. (Be sure to give it an awesome name like "The Jane Doe Fund for Paperclip Maximization" because how many chances do you have to name an organization after yourself?)  Once created, you can contribute money when you feel like it and deduct those contributions from your taxes. Your contributions will sit in an account accruing interest until you decide to write a grant to a specific charity.

There are interesting questions about when to put money in a DAF vs. donate directly, but if you are uncertain about the most effective charity, especially if you're so uncertain that you might not donate at all, you should create a DAF.

Creating Your DAF

Most major investment organizations allow you to create a DAF, such as Fidelity, Charles Schwab and Vanguard as well as most local community foundations (if you search for "community foundation" in a standard search engine, you should be able to find one near you). Be sure that you're able to invest in a no-load index fund (professional investors don't do better than chance, so it's not worth paying them a management fee). The major DAF hosts all provide this, so the only real consideration is the management fee they charge. I've found them to be pretty similar, so I just chose Fidelity since my retirement account is already there.

Put a few key details into their form and Voilà! You have your own fund!

What if I don't have $5,000?

The main reason why a DAF might not be right for you is that they require a minimum starting donation of $5,000. If you aren't able to put in $5,000 right away, look into other options that community foundations provide. For example, the foundation near me has an "Acorn fund", which allows you to donate smaller amounts of money over a longer period of time. 

Conclusion

I consider myself to be more informed than average about the subject of charity effectiveness, but if you look at my 80,000 Hours profile you can see I put all my donations into a DAF. Because even similar-sounding charities can vary in effectiveness by orders of magnitude, it's extremely important to think through your decisions. By using a DAF you can build the "habit" of altruism and take the tax advantages while still ensuring that your money goes to the most effective causes.

Why Classical Utilitarianism is the only (Archimedean) Ethic

Probably the most famous graph in ethics is this one of Parfit's:



He's constructing a series of worlds where each one has more people, but those people have a lower level of welfare. The question is whether the worlds are equivalent, i.e. whether it's equivalent to have a world with a huge number of barely happy people or a world with a small number of ecstatic individuals.

Classical utilitarianism answers "Yes", but some recent attempts to avoid unpleasant results (such as the "repugnant conclusion") have argued "No". For example, Parfit says:

Suppose that I can choose between two futures. I could live for another 100 years, all of an extremely high quality. Call this the Century of Ecstasy. I could instead live for ever, with a life that would always be barely worth living. Though there would be nothing bad in this life, the only good things would be muzak and potatoes. Call this the Drab Eternity. I believe that, of these two, the Century of Ecstasy would give me a better future.

The belief that the "Century of Ecstasy" is superior to the "Drab Eternity", no matter how long that eternity lasts, has been called "Non-Archimedean" by Arrhenius, in reference to the Archimedean Property of numbers, which says roughly that there are no "infinitely large" numbers.¹ Specifically, a group is Archimedean if for any $x$ and $y$ there is some $n$ such that $$\underbrace{x+x+\dots+x}_{\text{n times}}>y$$
The following remarkable fact is true:

Classical Utilitarianism is the only Archimedean ethic.

This means that if we don't accept that the briefest instant of a "higher" pleasure is better than the longest eternity of a "lower" pleasure, then we must be classical utilitarians.

Proof

First, define the terms. As always, we assume that there is some set $X$ which contains various welfare levels. There is an operation $\oplus$ which combines welfare levels; the statement $x\oplus y=z$ can be read as "A life with welfare $x$ and then welfare $y$ is equivalent to having a life with just welfare $z$."² It is assumed that this constitutes a group, i.e. the operation is associative and inverses and an identity exist.

In order to make decisions, we need some ranking; the statement $x>y$ means "The welfare level $x$ is morally preferable to $y$." We require $>$ to agree with our operation, i.e. if $x>y$ then $x\oplus c > y\oplus c$ for all $c$.

With the stipulation that our group is Archimedean, this reduces to a theorem of Hölder's, which states that all Archimedean linearly ordered groups are isomorphic to a subgroup of the reals under addition, i.e. classical utilitarianism. The proof is rather involved, but a fairly readable version can be found here.∎

Discussion

In order to be useful, non-Archimedean theories can't just say that there is some theoretical amount of welfare which is lexically superior - this level of welfare must exist in our day-to-day lives. Personally, when comparing a brief second of happiness on my happiest day to years of moderate happiness, I would choose the years. This leaves me with no choice but to accept classical utilitarianism.

Footnotes

1. Ethics with this property have also been called "discontinuous" or having a "lexical" priority.
2. Unlike in past blogs where I used $\oplus$ to be a population ethic, here I define it in terms of intra-personal welfare to fit more in line with Parfit's quote.

Group Theory and the Repugnant Conclusion

A fundamental question in population ethics is the tradeoff between quantity and quality. The world has finite resources, so if we promote policies that increase the population, we do so at the risk of decreasing quality of life.

Derek Parfit is credited with popularizing the importance of this problem when he pointed out that any population ethic which obeys some seemingly reasonable constraints must end up with what he called "the repugnant conclusion" - the conclusion that a world full of miserable people is better than a sparsely-populated world full of happy people. Since Parfit, there have been a range of theories seeking to preserve our intuitions about ethics while still avoiding this conclusion.

One discovery of abstract algebra is that we can understand the limitations of systems based solely on the questions they are able to answer, even if we don't know what the answers are.

Here, I'll consider any system capable of answering a question like "Are two people who each live 50 years morally equivalent to one person who lives 100 years?" (Again, we don't require that the answer be "Yes" or "No", but merely that there be some answer.) For notational ease, I use the symbol $\oplus$ to be the "moral combination", e.g. the above question can be written $$(50\text{ years})\oplus(50\text{ years})=100\text{ years?}$$ Such a system I will call a "moral group" and require that it obey a few standard requirements. These are:

1. Any two people can be replaced with one who is (significantly) better off
2. There is some level of welfare which is "morally neutral", i.e. a person of that welfare neither increases nor decreases the overall moral desirability of the world.
3. For any level of welfare, no matter how high, there is some level of welfare which is so negative that the two cancel out

With this definition, we have an impossibility theorem:

Theorem: In any "moral group", the repugnant conclusion holds.

Proof: Suppose that $x$ is a welfare level that is better than "barely worth living". Formally, say that there must be some $y$ where $0 < y < x$, i.e. it's possible to be worse off than $x$ and still have a "life worth living". We'll show that a world with just $x$ is morally equivalent to a world with two people who are both worse off than $x$. Repeating this ad infinitum leads to the conclusion that a world with a few happy people is equivalent to a world with a large number of people whose lives are "barely worth living."

Choose some $y$ between $0$ and $x$ (one exists, by the definition of $x$). Note that $x=y\oplus z$ where $z=y^{-1}\oplus x$, so we just need to show that $z<x$. Since $y>0$, $y^{-1} < 0$ because if it weren't then we'd have $y^{-1} > 0$; adding $y$ to both sides results in $0>y$ which contradicts the assumption that $y>0$. Therefore $y^{-1} \oplus x < x$, or to write it another way: $z < x$. So $x=y\oplus z$, with $y$ and $z$ both worse than $x$.

This means that for any world with people $x_1,x_2,\dots$ of high welfare, there is an equivalent world $y_1,y_2,\dots$ with more people, each of whom have lower welfare. By adding some person of low (but still positive) welfare $y_{n+1}$ to the second world, it becomes better than the first, resulting in the repugnant conclusion.∎

Algebra and Ethics

Symmetry is all around us. The kind of symmetry that most people think of is geometric symmetry, e.g. an equilateral triangle has rotational symmetry:

I've rotated the triangle by 1/3 of a rotation, but it remains the "same", just with a "relabeling" of the points. Hence this rotation is a symmetry of the triangle.

Ethical positions generally express another type of symmetry; when someone argues for "marriage equality" what they mean is that the gender of partners is merely a "relabeling" that keeps the important aspects like love and commitment the same. Symmetries in pain processing between humans and other animals has lead thinkers like Richard Dawkins to declare that species is merely a relabeling, and that causing pain to a cow is "morally equivalent" to causing pain to a human, calling our eating practices into question.

In 1854 Arthur Cayley gave the first modern definition of what mathematicians call a "group", and showed that groups are essentially permutations, thus establishing the theory of groups as the language of symmetry. Despite the importance of groups to symmetry and the importance of symmetry to ethics, I'm not able to find any ethical works based on group theory. So I hope to give what may be the first ever group-theoretical proof of ethics.

"Group-like" Ethics
I'm going to be concerned with questions like "is having two people, each of whom live 50 years, equivalent to having one person who lives 100 years?" I don't require that this question be answered either "yes" or "no", but only that the question has some answer.

So that this post doesn't take up a huge amount of space, I'm going to define the symbol $\oplus$ to mean "moral combination" and $=$ to mean moral equivalence, so the statement "two people, each of whom live fifty years, is equivalent to one person living 100 years" can be written as $$(50 \text{ years})\oplus(50 \text{ years})=100 \text{ years}$$ There are many different ways to define $\oplus$. For example, we might care only about the worst-off person - in this case $(50 \text{ years})\oplus(50 \text{ years})=50 \text{ years}$ as the worst-off person on the left-hand side of the equation has the same length of life as the worst-off person on the right. Alternatively, we might point out that quality of life degrades as you get older, so in fact maybe $(50 \text{ years})\oplus(50 \text{ years})=150 \text{ years}$ since the two young people get so much more joy out of their life. The World Health Organization follows this model and weights lives like this:

According to their formula, old age is so awful that $(40 \text{ years})\oplus(40 \text{ years})=125 \text{ years}$ and one person would have to live for thousands of years to be equivalent to two 50 year lifespans.

In addition to requiring that statements like $(50 \text{ years})\oplus(50 \text{ years})$ have some answer, I will also require that there is an "identity", i.e. there is some quality of life such that adding a person with that quality of life doesn't change the overall value of the world. This is a reasonable assumption because:

1. Sometimes increasing the population is a good idea, i.e. there is some $y$ such that $x\oplus y > x$
2. Sometimes increasing the population is a bad idea, i.e. there is some $z$ such that $x\oplus z < x$
3. By the intermediate value theorem, there must therefore be some value which I'll call $0$ such that $x\oplus 0 = x$

Any ethical system which has an operation like $\oplus$ I will call "group-like" (although observant readers will note that I'm making fewer assumptions than what groups require - technically this is a "unital magma").

"Utilitarian-like" Ethics
The classic definition of "utilitarianism" is to look only at happiness and to define $\oplus=+$, e.g. two people with five "units" of happiness is equivalent to one person with ten units of happiness.

There are a plethora of "utilitarian-like" ethical theories which define $\oplus$ as being sort of like addition, but not really. For example, negative utilitarians would first discard any pleasure, and look only at the pain of each individual before doing the addition. Prioritarians wouldn't completely disregard pleasure, but they would weight helping those in need more strongly. The Sen social welfare function weights income by inequality before doing the addition. And so on.

I will describe an ethical system as "utilitarian-like" if it is equivalent to doing addition with some appropriate transformation applied first. Formally, utilitarian-like operations are of the form $x\oplus y = f(x)+f(y)$.

The Theorem
With these definitions in mind, we can state our theorem:

The only ethical system which is both group-like and utilitarian-like is classical ("Benthamite") utilitarianism.

Observant readers will notice that my examples in the "group-like" section were different than the examples in the "utilitarian-like" section. This theorem proves that this is not an accident.

Proof: $x\oplus 0 = f(x)+f(0)$ so $x = f(x)+f(0)$ or to rewrite it another way, $f(x)=x - f(0)$ where $f(0)$ is some constant. This means that all group-like and utilitarian-like functions are equivalent, just shifted slightly. To use a formal definition of "equivalent", the homomorphism $\phi(x) = x + f(0)$ can be easily seen via the first isomorphism theorem to be an isomorphism $(\mathbb{R},\oplus)\to(\mathbb{R},+)$.∎

Discussion
The reason why Prioritarians et al. fail to be group-like is something I haven't seen discussed much in the literature: a lack of an identity element.

For example, suppose $x\oplus y = f(x)+f(y)$ where $$f(x) = \left\{
\begin{array}{lr}
2x & x < 0\\
x & else \end{array} \right.$$ This is a negative utilitarian-type ethics which weights suffering (i.e. negative experience) more strongly.

Consider a few possible worlds in which we add someone of utility 2:

1. $-1\oplus 2 = 0$
2. $-2\oplus 2 = -2$
3. $-3\oplus 2 = -4$

In the first case, adding someone of utility two improves the world. In the second, it keeps the world the same and in the third it makes the world worse.

That negative utilitarianism requires this isn't immediately obvious to me, and I believe it to be a non-trivial result of using group theory.

Conclusion
We might view negative utilitarianism or prioritarianism as a form of "pre-processing". For example, we might say that painful experiences affect utility more than positive ones. But when it comes to comparing utility to utility, it must be "each to count for one and none for more than one" with all the counter-intuitive results that implies.